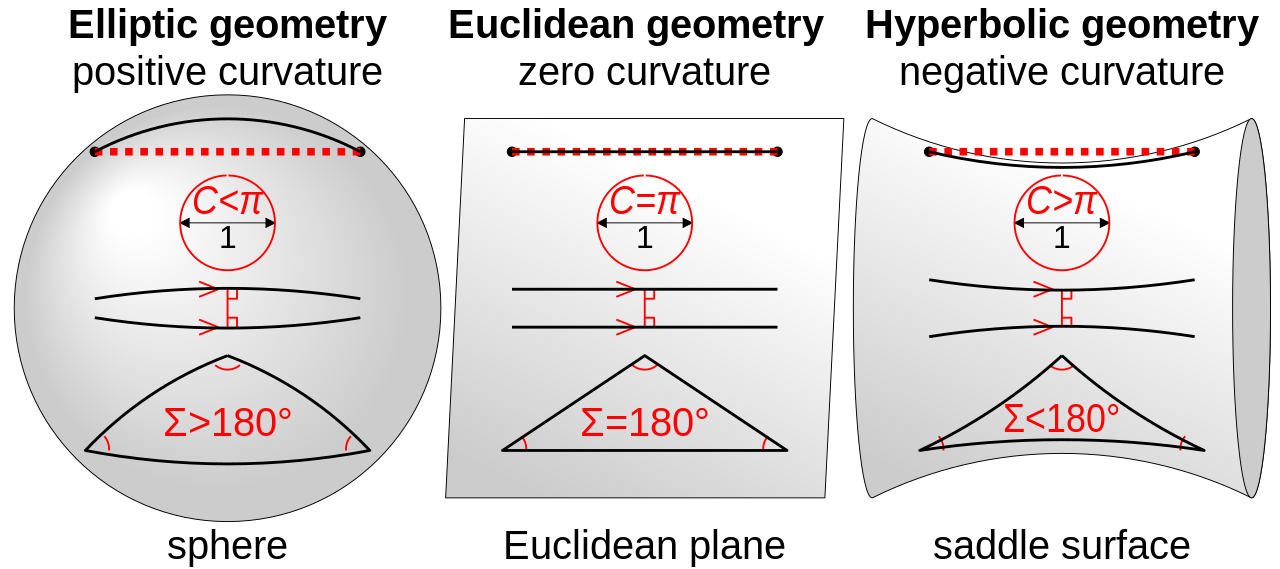
The three main non-hybrid geometries currently recognized in mathematics.
Source: Comparison of Geometries, Cmglee (Wikipedia).
We may not think about it very often, but space has a shape. Relatively speaking, at least. It doesn't "have a shape" in the sense that we're used to, but it does have form. Space doesn't look like a cube because cubes have edges, and as far as we know, "space" is infinite and/or constantly expanding. Beyond the astronomical sense (anything outside of Earth's atmosphere), space itself (the empty distance between things) is just… space. It's something, or rather, nothing, waiting to be filled.
Now, assuming boundaries are present, 1D is a line, 2D is a plane, 4D would be a tesseract, etc. Three-dimensional, Euclidean space has no known boundaries, but if it did, it would be a cube. And since it doesn't, it merely has the ability to house "regular" cubes. "Shape" means either the form of something or the description of an object.
But that is only Euclidean geometry. Non-Euclidean 3D geometry might be shaped like a 2D sphere (elliptical geometry), or a Pringle (hyperbolic geometry). In elliptical geometry (very small, as spheres are closed surfaces), parallel lines would converge. In hyperbolic geometry (discrete but extendable), parallel lines would diverge. And in conventional Euclidean geometry, as we know, parallel lines fall right in the middle.
One major difference between Euclidean and non-Euclidean geometry is the properties that angles possess. Like each of the 8 cubes that make up a tesseract/hypercube, 90 degree angles will appear to be irregular, to not follow familiar rules, in non-Euclidean geometry. However, they will still be 90 degree angles, even if they look too small or too large to be this way. This is because space is simply shaped differently when it's not Euclidean, and so everything it contains will be shaped differently as well.
But angles are only one of the many interesting topics to explore whose principles are changed by the laws of their geometry. Let's break it down.

The three main non-hybrid geometries currently recognized in mathematics.
Source: Comparison of Geometries, Cmglee (Wikipedia).
I have been calling this geometry elliptical, but there are actually two kinds. First, elliptical. Second, double elliptical, also known as spherical. Assume that I am talking about "single" elliptical when I say elliptical.
Properties of Elliptical and Spherical Geometry
A few features of elliptical/spherical geometry include:
But there is a main difference between these systems: in elliptical geometry, parallel lines intersect at only one point. In spherical/double elliptical geometry, they intersect at two points.
Before I follow this up with some good old Wikipedia (slightly edited for easier reading), since they explain it much better than I do, I must define a few words first:
Wikipedia, on antipodal points:
In elliptical and spherical geometry, two lines perpendicular to a given line must intersect. In fact, the perpendiculars on one side [of that given line] all intersect at a single point, called the "absolute pole" of that line. The perpendiculars on the other side also intersect at a point. However, unlike in spherical geometry, the absolute poles on either side of an elliptical geometry are the same. This is because there are no antipodal points in elliptical geometry. For example, this is achieved in the hyperspherical model by making "points" in Euclidean geometry actually be pairs of opposite points when on a sphere. The reason for doing this is that it allows elliptical geometry to satisfy the axiom that there is a unique line passing through any two points.
This happens because, unlike in spherical geometry, two points on opposite sides of the ellipse are identified, meaning they are one and the same.
Hyperbolic geometry is another type of non-Euclidean geometry; instead of positive curvature, it has negative curvature. We would call this a saddle shape, or, more informally, a Pringle. It is the inside of a sphere instead of the exterior, like elliptical.
Hyperbolic geometry is based on hyperbolas. A hyperbola is similar to a parabola in that it is a conic section (fits on a section of a cone), but a hyperbola has two curves (called "branches") instead of one. Also, hyperbolas are the only conic sections with asymptotes.
Asymptotes are the boundaries of a function that a curve may approach but never touch, and definitely never cross. In other words, a curve is tangent to its asymptote only at a point at infinity. In my opinion, asymptotes are both infuriating and satisfying to look at on a graph.
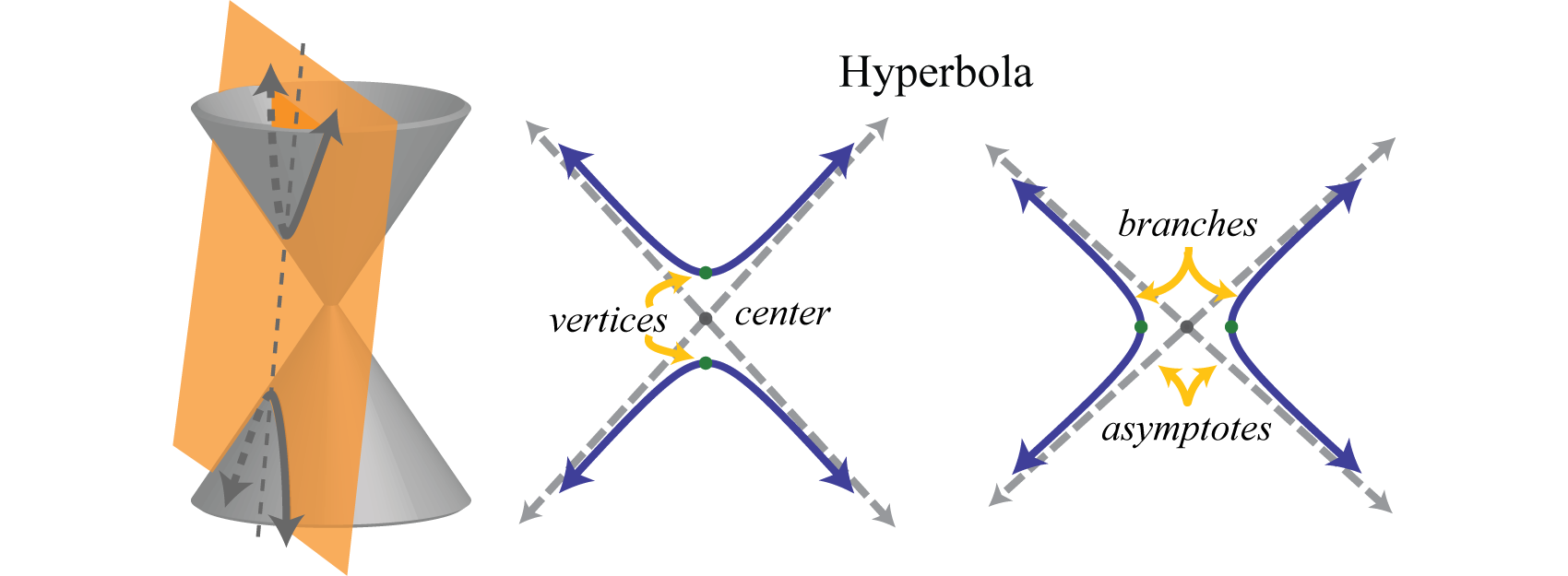
A hyperbola, represented on cones.
Source: Hyperbolas, saylordotorg on GitHub.
In comparison to other conic sections:
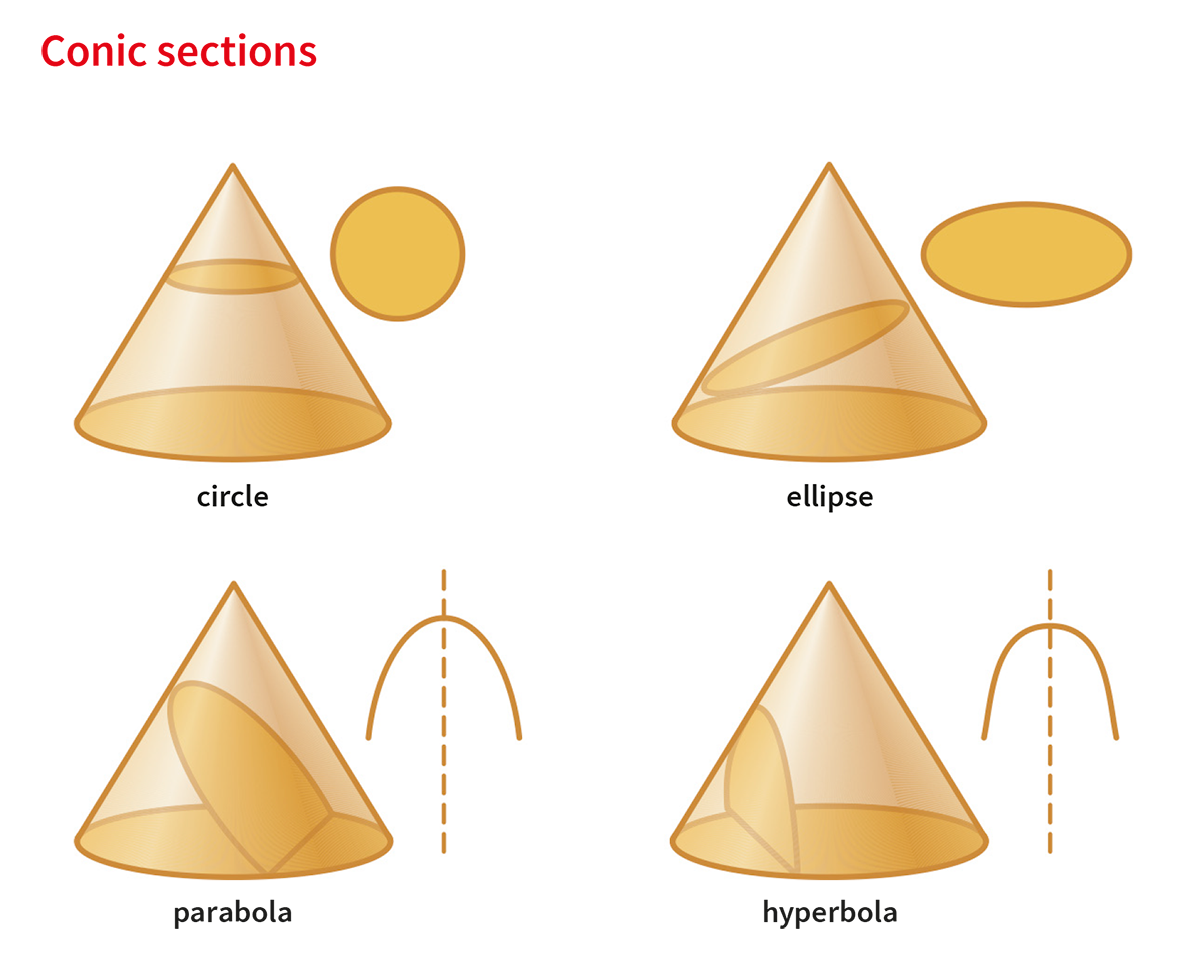
(This image only shows half of its mentioned hyperbola; see the other image for a true representation of a hyperbola on cones.)
Source: Oxford Learner's Dictionaries.